Overview
정렬 문제는 임의의 배열이 주어졌을때, 규칙에 맞게 정렬된 배열을 만드는 문제이다. 이번 장에서 다룰 정렬 알고리즘은 Merge sort, Quick sort, Heap sort이다. Merge sort와 Quick sort는 Divide & Conquer기법을 사용하는 대표적인 정렬법으로 매우 중요하고 자주 언급된다.
합병 정렬(Merge sort)
합병 정렬(Merge sort)는 분할 정복(Divide & Conquer) 패러다임의 대표 알고리즘이다.
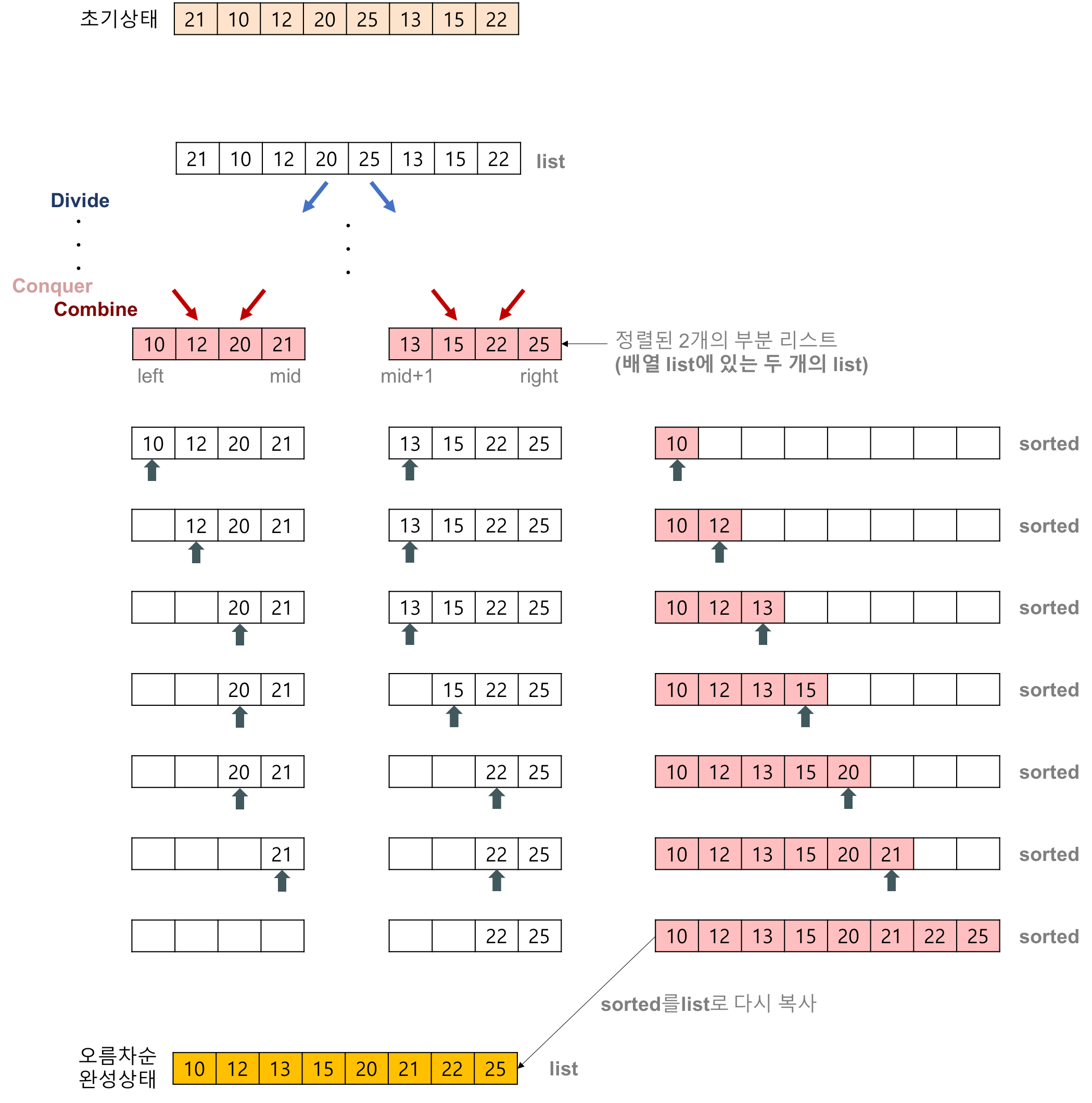
분할 정복 알고리즘은 보통 세 가지 구성된다. Divide, Base, Conquer가 그것 인데 합병 정렬에서 Divide는 정렬되지 않은 배열을 절반으로 나누는 작업을 한다. Base는 더 이상 나누어지지 않는 과정에 이르러 Divide 단계을 멈추고 Conquer 단계로 넘어가는 단계이다. Conquer는 더이상 나누어지지 않는 배열들을 합쳐 가면서 정렬된 배열을 만들어 가는 단계이다. 참고로, Base 단계에서 배열의 길이가 0 또는 1이면 더이상 나누어지지 않는 배열로 여긴다.

아래 그림은 정렬된 두 리스트({10,12,20,21}, {13,15,22,25})를 병합하여 하나의 정렬된 리스트를 만드는 과정을 나타낸다. 정렬된 2개의 리스트를 병합하는데는 $O(n)$의 복잡도로 처리가 가능하다는 것이 중요하다.
합병 정렬(Merge Sort)의 시간복잡도

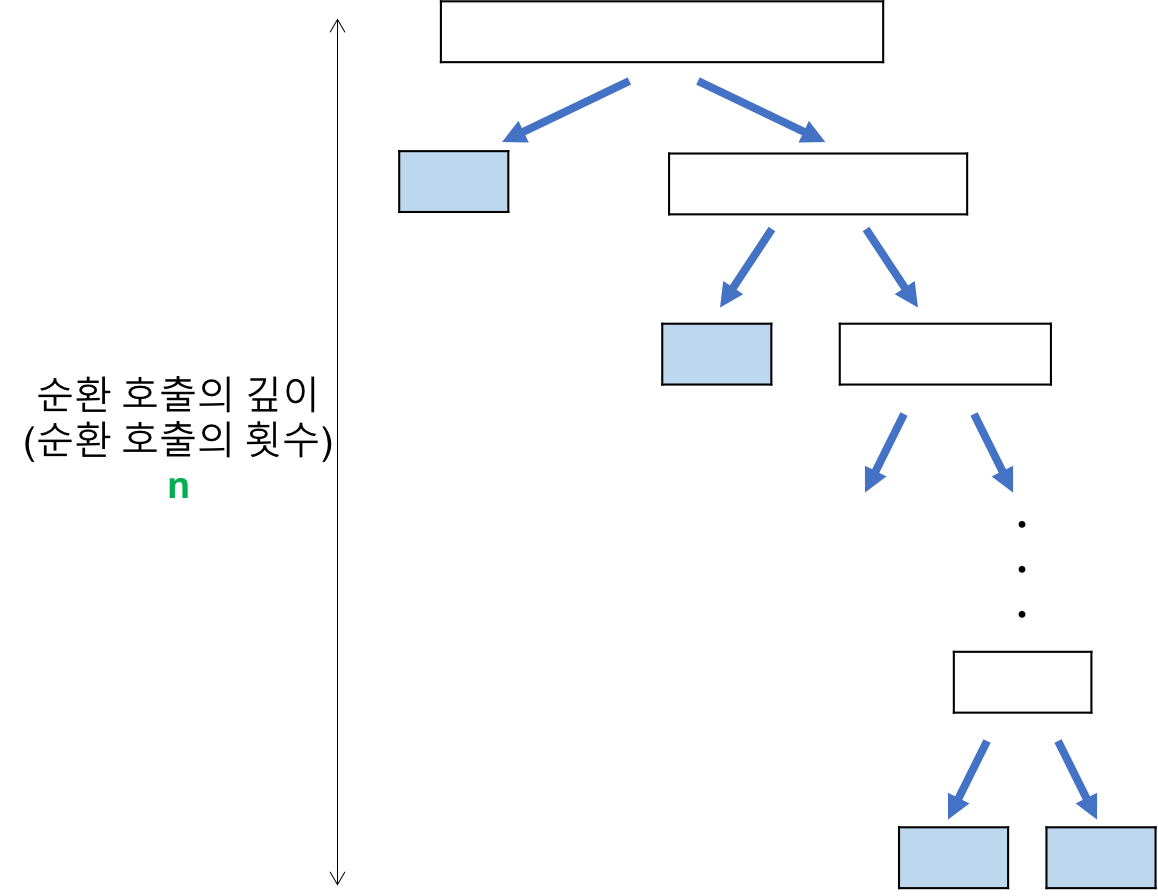
트리의 레벨(k)마다 n번의 비교가 일어난다. 따라서 합병 정렬의 복잡도는 $k*n$ 이고 k는 트리의 높이만큼인 $\log_2n$ 이다. 최종적으로 합병정렬의 복잡도는 $O(n\log_2n)$이다.
합병 정렬(Merge Sort)의 특징
- 데이터의 분포에 영향을 덜 받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다. (O(nlog₂n)로 동일)
- 만약 레코드를 연결 리스트(Linked List)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다. 따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 졍렬 방법보다 효율적이다.
- 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하다. 즉 제자리 정렬(in-place sorting)이 아니다.
- 제자리 정렬(in-place sorting)로 구현할 수 있다.
퀵 정렬(Quick Sort)
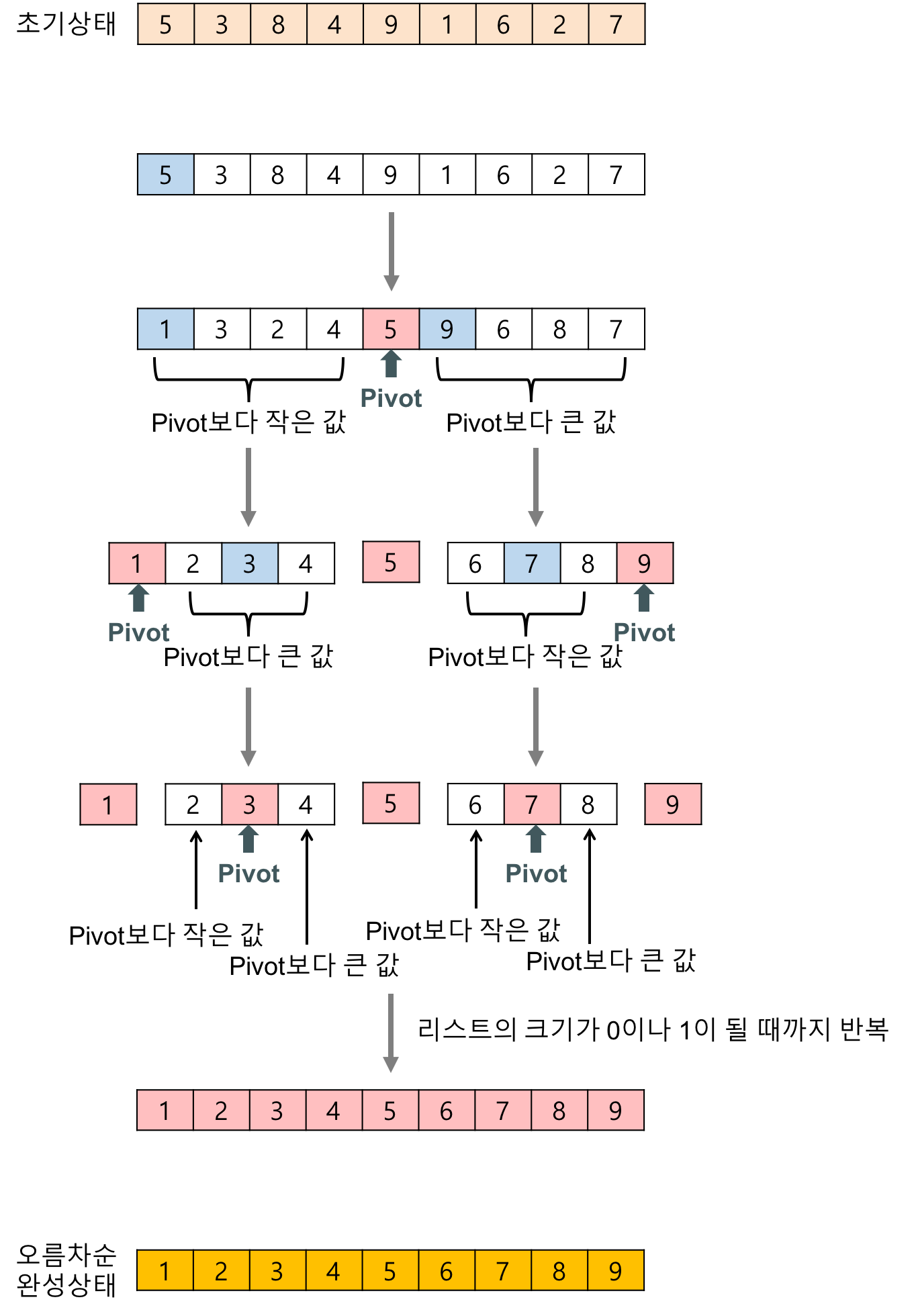
분할 정복 패러다임을 활용한 알고리즘으로, 평균적으로 빠른 정렬방법이다. 합병 정렬과 달리 퀵 정렬은 리스트를 나누는 Divide 단계에서 균등하게 나누지 않을수도 있다. 왜냐하면 퀵정렬은 리스트에 있는 한 요소를 선택하고 이 값을 기준으로 리스트를 나눈다. 이 요소를 피벗(pivot) 이라고 하며 보통 리스트의 제일 앞에있는 요소를 선택한다. 리스트를 나눌때, 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮기고 피벗보다 큰 요소들은 피벗의 오른쪽으로 옮기는 방식으로 리스트를 나눈다. 그렇게 리스트를 나누다가 크기가 0이나 1 된 시점이 마침내 Base단계이다.
퀵 정렬의 특징
- 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
- 퀵 정렬의 불균형 분할을 방지하기 위하여 피벗을 선택할 때 더욱 리스트를 균등하게 분할할 수 있는 데이터를 선택하는게 성능에 좋다.
퀵 정렬의 시간복잡도
퀵 정렬의 평균적인 시간복잡도는 $O(n\log_2n$)이다.
$$T(n) = 2T(\frac{n}{2}) + n$$
$$... + 4(\frac{n}{4})+2(\frac{n}{2})+n$$
덧셈항의 값이 n이고 덧셈항이 $\log_2n$개 만큼 있기 때문에 시간복잡도는 $O(n\log_2n$)가 된다.

아래 그림은 최악인 경우를 나타낸다. 이때 시간 복잡도는 $O(n^2)$이다.
$$T(n) = T(n-1) + n$$
$$ 1 + ... + n-1 + n = \cfrac{n(n+1)}{2}$$
힙 정렬(Heap sort)
힙정렬을 이해하기에 앞서 먼저 힙(Heap)이 무엇인지 정리할 필요가 있다. 참고로 Heap의 사전적 의미는 더미, 무더기라는 의미이다.
Heap(자료구조)
힙은 여러 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다. 최대값을 빠르게 찾아내는 힙을 최대힙(max heap), 최소값을 빠르게 찾아내는 힙을 최소힙(min heap)이라고 한다.
최대 힙(max heap)은 모든 부모 노드의 값이 자식 노드의 값보다 크거나 같은 규칙을 만족하는 완전 이진 트리(Complete Binary Tree)를 말한다. 반대로 최소 힙(min heap) 모든 부모 노드의 값이 자식 노드의 값보다 작거나 같은 완전 이진 트리(Complete Binary Tree)이다. 참고로 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)

Binary Tree(이진트리)
이진트리는 자식노드가 최대 두 개인 노드들로 구성된 트리이다. 이러한 이진트리에는 정이진트리(Full Binary Tree), 완전이진트리(Complete Binary Tree), 균형이진트리(Balanced Binary Tree) 등이 있다.
정이진트리(Full Binary Tree) - 모든 노드가 0 아니면 2개의 자식만을 가지는 트리.
완전이진트리(Complete Binary Tree) - 가장 아래 두 레벨에 있는 노드들을 제외한 모든 노드들이 두개의 자식 노드를 가진다. 그리고 가장 아래 레벨에서 노드는 왼쪽에서 오른쪽으로 채워져야 한다.
힙정렬 구현
힙정렬은 최대힙이나 최소힙을 구성하여 정렬하는 것이다. 힙 정렬을 구현하는데는 크게 삽입(add), 삭제(remove) 두 가지 메서드를 구현해야 한다.
삽입(add)
힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.

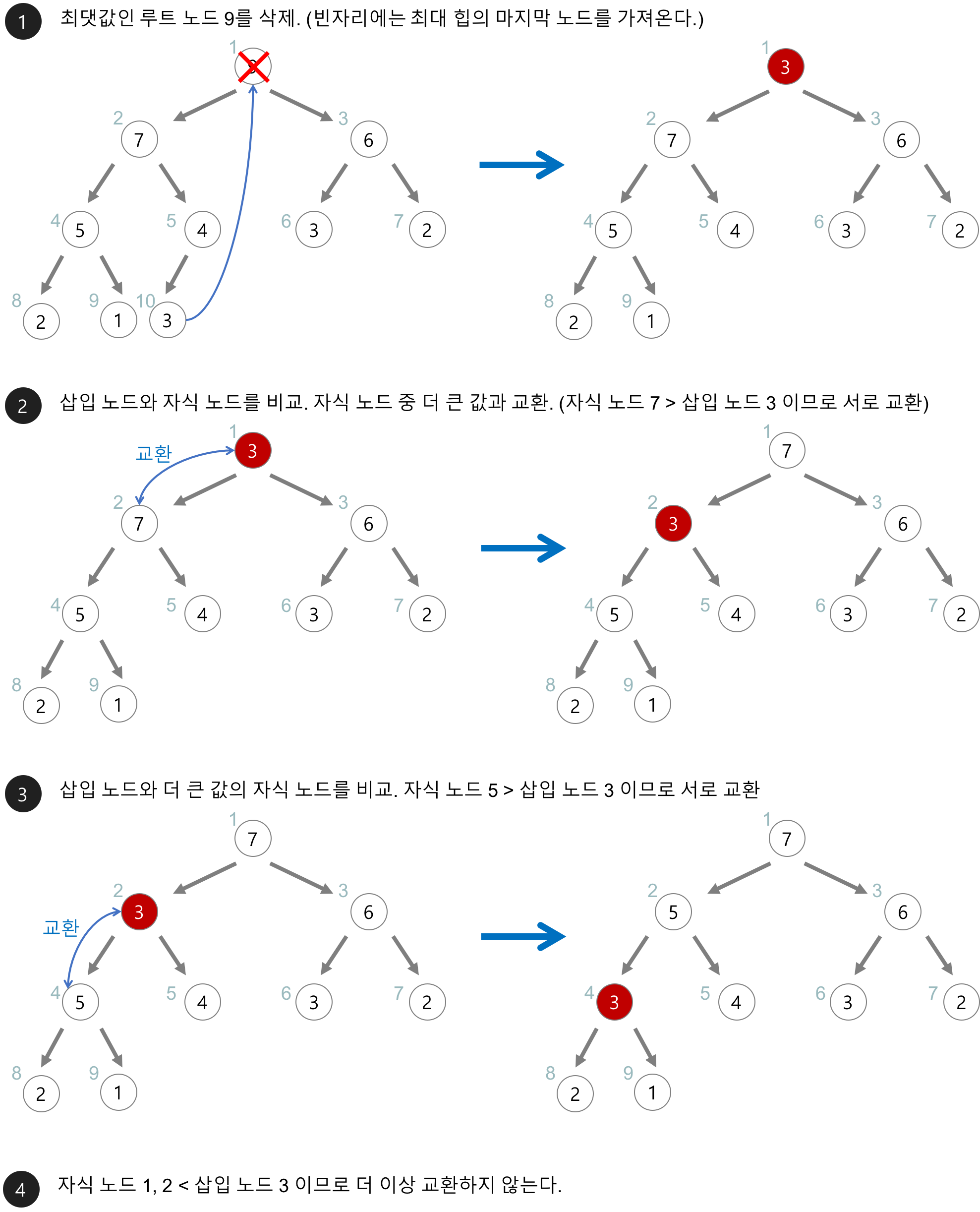
삭제(remove)
최대 힙(max heap)에서 삭제 연산은 최댓값을 가진 노드를 삭제하는 것이다. 최댓값을 가진 노드는 루트 노드이므로 루트 노드가 삭제한다. 그리고는 힙의 규칙에 맞게 노드들을 재구성한다.
힙 정렬(Heap Sort)의 시간복잡도
힙 트리의 전체 높이가 거의 log₂n(완전 이진 트리이므로)이므로 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재정비하는 시간이 log₂n만큼 소요된다. 그런데 데이터의 갯수가 n 이므로 전체적으로 O(nlog₂n)의 시간이 걸린다.
마치며
우리는 Selection Sort, Insertion Sort, Bubble Sort, Merge Sort, Quick Sort, Heap Sort의 총 6가지의 정렬 알고리즘을 개념, 특징, 시간복잡도로 나누어 공부했다. 기본적인 알고리즘들이지만 면접이나 기초를 다지는데는 아주 좋은 알고리즘이다. 또한, 알고리즘 패러다임 중 하나인 분할정복 방법이 적용된 좋은 예시이므로 복습하는 습관을 가지자.
알고리즘 성능 비교

'수학 > Algorithms' 카테고리의 다른 글
| 동적 계획법 [DP] (0) | 2024.12.29 |
|---|---|
| P-NP 문제 (0) | 2021.01.24 |
| Class P & Class NP (0) | 2021.01.24 |
| 알고리즘의 복잡도 (1) | 2021.01.17 |
| 정렬 알고리즘(Selection sort, Insertion sort, Bubble sort) (1) | 2021.01.11 |