Introduction
우리는 P문제와 NP문제를 정의를 알아보았다. 2021/01/24 - [IT/Algorithms] - Class P & Class NP
간단히 다시 정리하자면 아래와 같다.
P문제 - 다항시간안에 풀 수 있는 판별문제 (결정적/비결정적 알고리즘 모두)
NP문제 - 비결정적 알고리즘으로 다항시간안에 풀 수 있는 판별문제
P문제는 우리에게 익숙한 결정적 알고리즘으로 해결이 가능한 문제들이다. 그리고 P문제는 비결정적 알고리즘으로도 충분히 해결이 가능한 문제이다. (결정적 알고리즘은 비결정적 알고리즘의 조금 특수한 경우) 따라서 ClassP로 분류된 문제들은 Class NP에도 포함된다. (예를 들어, 합성수 판별문제는 P문제이면서 동시에 NP문제이다.)
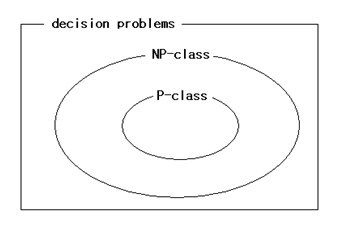
위 그림은 Class P와 Class NP의 집합 관계를 나타내는 그림이다. 그럼 역으로 Class NP는 Class P에 포함될까? 다른 말로 모든 NP 문제는 P문제일까? 이 질문 자체가 바로 P-NP 문제이다.
학자들은 P-NP문제를 수학적으로 해결하기 위해 NP-난해(NP-hard)와 NP-완전(NP-completeness)개념을 도입하였다. 하나씩 천천히 알아보자.
NP-난해(NP-hard)
NP-난해: 모든 NP 문제들을 다항시간 환원(polynomial-time reduction) 시킬 수 있는 문제의 집합
NP-난해를 이해하는데 가장 중요한 개념은 환원(reduction)이다. (주의: NP-난해는 판별(decision)문제에만 국한되지 않음)
환원(reduction)
환원은 한 문제를 다른 문제로 전환하는 것을 말한다. 환원은 서로 다른 두 문제의 난이도를 비교하는 데 자주 사용된다.
아래의 두 문제를 보고 어떤 문제가 더 어려운지 그 난이도에 대해서 생각해보자.
문제 A: 주어진 n개의 숫자에서 중간값을 계산
문제 B: 주어진 n개의 숫자를 크기 순서로 정렬
정답 먼저 이야기하자면 문제 B가 문제 A보다 더 어렵고, 문제 A를 문제 B로 환원할 수 있다.
문제의 난이도 관점에서 사실문제 A는주어진 숫자들을 정렬하고, 그 가운데에 있는 수를 뽑으면 풀리는 문제이다. 즉 문제 B를 해결하면 , 문제 A도 쉽게 풀 수 있다는 말이기 때문에, 문제 B의 난이도가 문제 A보다 높다고 할 수 있다.
알고리즘의 관점에서는 문제 A를 해결하는 알고리즘에 문제 B를 해결하는 알고리즘을 포함시키면 문제 A를 간단히 해결할 수 있다. 이 상황을 문제 A는 문제 B로 환원이 된다고 표현한다. 즉 어떤 문제의 본질에 가까운 보다 어려운 문제를 보다 중점적으로 다루게 된다.
다항시간 환원(polynomial-timereduction)
위 그림은 앞서 예제로 보았던 문제 A를 문제 B로 환원시키는 것을 도식화했다. 사실 이러한 환원 과정에서는 문제 A와 문제 B의 입출력을 맞춰주기 위한 추가 계산 함수인 $f, g$가 필요하다. 그리고 이 함수들의 다항시간 내에 수행된다면 우리는 이러한 환원을 다항시간 환원(polynomial-time reduction)이라 한다.
다항시간 환원(polynomial-time reduction) - 환원시 문제 A와 B의 입출력을 맞추어주기 위한 함수 f, g가 다항식 시간 내에 계산되는 환원
자 이렇게 우리는 NP-난해의 가장 중요한 개념인 다항시간 환원을 이해했다. 다시 NP-난해 문제의 정의 되짚어 보자.
NP-난해의 정의는 '모든 NP 문제를 다항시간 환원(polynomial-time reduction)'시킬 수 있는 문제였다.
즉, 존재하는 모든 NP문제를 환원시키는 문제들이 NP-난해문제이다. 이름에서 보듯이 NP-난해 문제들은 모든 NP문제들 보다 어려운 문제 집합이다.
NP-완전(NP-completeness)
NP-완전: 문제 스스로가 NP문제이면서, 모든 NP 문제를 다항시간 환원(polynomial-time reduction)시킬 수 있는 문제

위 그림은 모든 NP 문제들에 대한 다이어그램이다. NP-완전은 스스로가 NP문제이기 때문에 당연히 NP문제에 포함된다. 그리고 NP-완전은 정의에 따라 모든 NP 문제를 환원시킬 수 있다. 즉 NP문제를 해결하는데 NP-완전을 해결하는 알고리즘을 사용할 수 있다는 이야기다.
다르게 표현하자면, 무수히 많이 존재할 수 있는 모든 NP문제를 해결하기에 노력하기보다는, 더 어렵고 문제의 본질에 가까운 NP-완전으로 그리고 만약에 우리가 이러한 어려운 NP-완전 문제들 중 단 하나만이라도 다항시간내에 풀 수 있는 결정적 알고리즘을 찾는다면, 모든 NP문제가 다항시간 안에 풀리게 되는 셈이다. 즉, P-NP 문제해결!
우리가 비결정적 문제를 다루며 접했던, 부분집합 합 문제은 사실 NP-완전이고 아래는 또 다른 NP-완전 문제의 다른 예이다.
- 충족 가능성 문제(satisfiability problem)
- 논리식이 주어졌을 때, 논리값을 참으로 만드는 변수 대입이 존재하는가.
- 해밀턴 경로(Hamiltonian path)
- 그래프가 주어졌을 때, 각 꼭지점을 한번씩만 지나는 경로가 존재하는가.
- 순회 세일즈맨 문제(traveling salesman problem)
- 각 변에 가중치가 주어진 그래프와 X가 주어졌을 때, 길이가 X 보다 작은 해밀톤 회로가 존재하는가
Conclusion
하지만 아쉽게도 아직 인류는 NP-완전 문제들 중에 다항시간내에 풀리는 결정적 알고리즘을 찾지 못했다. 그렇다면 우리는 현재상황을 P = NP인 경우와 P != NP인 경우 두 가지로 나누어서 생각해볼 수 있다.
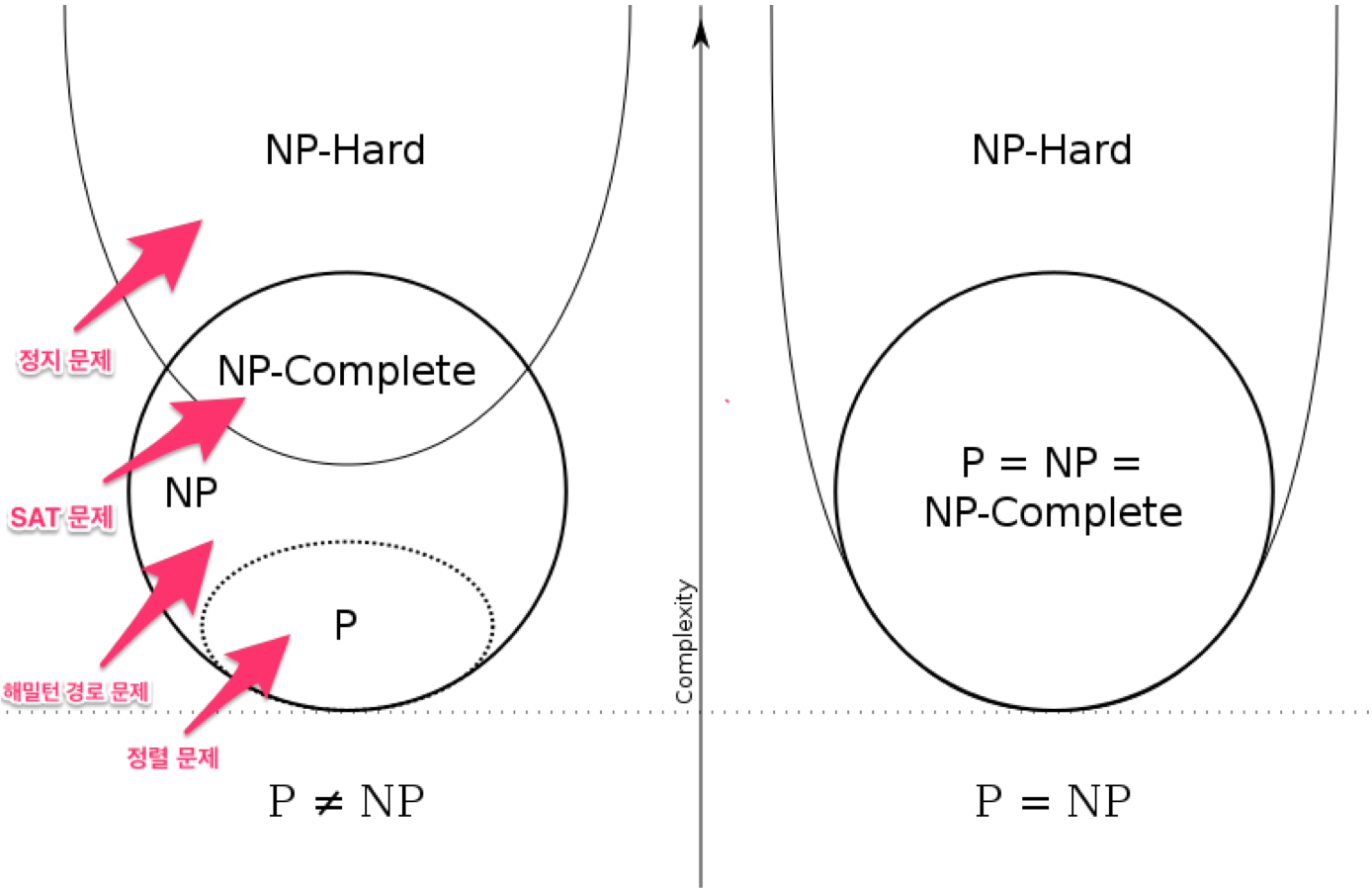
P != NP라면 어려운 문제를 다항시간내에 푸는 알고리즘을 찾을 수 없다는게 증명되어 어려운 문제는 다른 여러 방법을 모색하게 된다.(approximate 알고리즘) P = NP라면 NP문제를 전부 다항시간내에 풀 수 있고 기존의 모든 어려운 문제를 쉽게 풀 수 있게 된다.
'수학 > Algorithms' 카테고리의 다른 글
| 동적 계획법 [DP] - [Longest Increasing Subsequence] (0) | 2024.12.29 |
|---|---|
| 동적 계획법 [DP] (0) | 2024.12.29 |
| Class P & Class NP (0) | 2021.01.24 |
| 알고리즘의 복잡도 (1) | 2021.01.17 |
| 정렬 알고리즘(Merge sort, Quick sort, Heap sort) (0) | 2021.01.13 |
